Desafio! - Jogo Flash!
- SamWave
- Urangutango careca com franja na testa

- Mensagens: 2314
- Registrado em: Qua Dez 22, 2004 1:37 pm
- Sexo: Masculino
- Main Char: Samwave
- Contato:
Desafio! - Jogo Flash!
"O Lula é meu pastor........por isso estou pastando...."



- Terra Nova
- Macaco Admin

- Mensagens: 2347
- Registrado em: Ter Jul 29, 2003 11:23 pm
- Sexo: Masculino
- Lousy Aim
- Macaco Admin

- Mensagens: 1849
- Registrado em: Qui Jan 15, 2004 2:16 am
- Sexo: Masculino
- Contato:
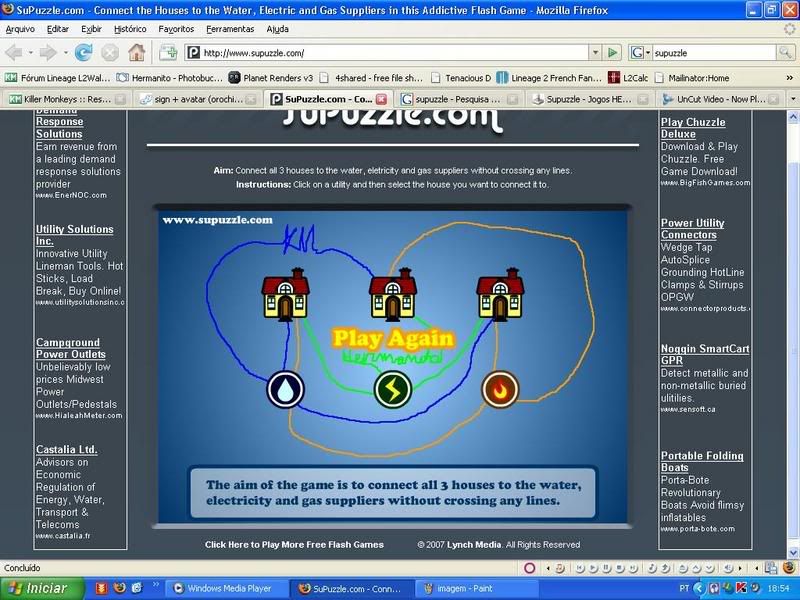
Até onde eu li, esse problema só tem solução num plano tridimensional, sendo que a solução bidimensional é impossível. Nesse site tem um bug que permite que você passe a linha do fonecedor (água, luz, gás) por outro fornecedor.
Essas informações eu tirei de um fórum, mas se o Pereira botar uma SS da solução dele aqui, eu posto lá e quebro as pernas dos caras...
E aí Pereira, tem a manha de postar uma SS do jogo finalizado?
Essas informações eu tirei de um fórum, mas se o Pereira botar uma SS da solução dele aqui, eu posto lá e quebro as pernas dos caras...
E aí Pereira, tem a manha de postar uma SS do jogo finalizado?
- Hmto
- Urangutango careca com franja na testa

- Mensagens: 1716
- Registrado em: Dom Mai 29, 2005 3:44 am
- Sexo: Masculino
- Main Char: Monkeygirl
- Contato:
Impossivel???
qm disse??
eu consegui... pra provar tem atem o meu nick escrito Hermanito em verde...
e KM em azul...
http://uncutvideo.aol.com/videos/8b651a ... fab0d3ba0d
qm disse??
eu consegui... pra provar tem atem o meu nick escrito Hermanito em verde...
e KM em azul...

http://uncutvideo.aol.com/videos/8b651a ... fab0d3ba0d
- Lousy Aim
- Macaco Admin

- Mensagens: 1849
- Registrado em: Qui Jan 15, 2004 2:16 am
- Sexo: Masculino
- Contato:
Hermanito... esse menino.... como eu posso responder sem ser rude....
Releia meu post...
Releu? Então. Viu ali onde eu mencionei alguma coisa sobre um bug nesse site? Então... o bug deixa você passar uma das linhas por um fornecedor, o que pelas regras é proibido. No seu caso, você passou uma linha de gás (foguinho - linha laranja) por dentro do fornecedor de água (gotinha).
Não, não, não... não pode não!
Impossível sim. Quem disse? A fórmula de Euler: p - q + r = 2 onde p =
número de vértices, q = número de arestas (ou lados), r = numero de regiões. Esse problema, como eu já disse, se resolve somente no plano tridimensional.
Eu provo, mas tem que ler até o final.
Nós temos três fornecedores: A, B, C e 3 casas: 1, 2, 3
A B C
1 2 3
E temos que levar uma linha de cada fornecedor até todas as casas.
A prova é dada por contradição. Suponha que seja possível desenhar a figura sem nenhuma intersecção dos lados.
Somamos o número de lados no limite de cada região sobre todas as r regiões e chamamos esse número de N. Uma vez que nenhuma linha une uma letra (fornecedor) a outra e nenhum número (casa) a outro, então não existem triângulos de forma que N>=4r.
Para essa ilustração, pense num quadrado. A região interna possui 4 linhas e a região extrena também 4, portanto N=8. Se fosse um triângulo, então N seria 3+3=6, mas não existem triângulos nesse problema.
N conta cada lado NO MÁXIMO duas vezes (uma linha só pode ter 1 ou 2 regiões de cada lado), então N <=2q (=2x9=18)
Nós tínhamos N >= 4r, então 4r <= N <= 18
r <= 9/2 (=4.5) ......(1)
Aplicando a fórmula de Euler, p - q + r = 2
6 - 9 + r = 2
r = 5 ......(2)
Comparando (1) e (2) nós vemos que existe uma contradição e nossa suposição de que esta figura está num plano bidimensional é impossível. Por isso numeros e letras não podem ser unidos sem que haja pelo menos uma intersecção de linhas. Booyakasha!
NEXT!!
Releia meu post...
Releu? Então. Viu ali onde eu mencionei alguma coisa sobre um bug nesse site? Então... o bug deixa você passar uma das linhas por um fornecedor, o que pelas regras é proibido. No seu caso, você passou uma linha de gás (foguinho - linha laranja) por dentro do fornecedor de água (gotinha).
Não, não, não... não pode não!
Impossível sim. Quem disse? A fórmula de Euler: p - q + r = 2 onde p =
número de vértices, q = número de arestas (ou lados), r = numero de regiões. Esse problema, como eu já disse, se resolve somente no plano tridimensional.
Eu provo, mas tem que ler até o final.
Nós temos três fornecedores: A, B, C e 3 casas: 1, 2, 3
A B C
1 2 3
E temos que levar uma linha de cada fornecedor até todas as casas.
A prova é dada por contradição. Suponha que seja possível desenhar a figura sem nenhuma intersecção dos lados.
Somamos o número de lados no limite de cada região sobre todas as r regiões e chamamos esse número de N. Uma vez que nenhuma linha une uma letra (fornecedor) a outra e nenhum número (casa) a outro, então não existem triângulos de forma que N>=4r.
Para essa ilustração, pense num quadrado. A região interna possui 4 linhas e a região extrena também 4, portanto N=8. Se fosse um triângulo, então N seria 3+3=6, mas não existem triângulos nesse problema.
N conta cada lado NO MÁXIMO duas vezes (uma linha só pode ter 1 ou 2 regiões de cada lado), então N <=2q (=2x9=18)
Nós tínhamos N >= 4r, então 4r <= N <= 18
r <= 9/2 (=4.5) ......(1)
Aplicando a fórmula de Euler, p - q + r = 2
6 - 9 + r = 2
r = 5 ......(2)
Comparando (1) e (2) nós vemos que existe uma contradição e nossa suposição de que esta figura está num plano bidimensional é impossível. Por isso numeros e letras não podem ser unidos sem que haja pelo menos uma intersecção de linhas. Booyakasha!
NEXT!!
- SamWave
- Urangutango careca com franja na testa

- Mensagens: 2314
- Registrado em: Qua Dez 22, 2004 1:37 pm
- Sexo: Masculino
- Main Char: Samwave
- Contato:
Quando eu era muleque e estava na escola, eu costumava falar esse teste e o pessoal fazia no papel, ai a resposta (horas depois) eu falava q a eletricidade era pelo poste, nos cabos....e o resto por canos, logo a luz pode passar por cima....
Ai quando vi esse em flash, fiquei tentando descobrir como fazia até q deu certo...rs...
Hermanito deve ter usado o santo google...rs
Para quem não recorreu ao google, a dica é usar o botão direito...^^
Ai quando vi esse em flash, fiquei tentando descobrir como fazia até q deu certo...rs...
Hermanito deve ter usado o santo google...rs
Para quem não recorreu ao google, a dica é usar o botão direito...^^
"O Lula é meu pastor........por isso estou pastando...."



- Pereirao
- Macaco Admin

- Mensagens: 1806
- Registrado em: Qua Jan 07, 2004 10:17 am
- Sexo: Masculino
- Localização: São Paulo - SP - Brasil
- Contato:
Exato... Moleza!Lousy Aim escreveu:Até onde eu li, esse problema só tem solução num plano tridimensional, sendo que a solução bidimensional é impossível.
Quem não ri de si mesmo, deixa esse trabalho para os outros...
Existem 10 tipos de pessoas: As que entendem binário e as que não entendem...
"Cada um cava a cova que consegue subir" (Ze_ninguém)
- Hmto
- Urangutango careca com franja na testa

- Mensagens: 1716
- Registrado em: Dom Mai 29, 2005 3:44 am
- Sexo: Masculino
- Main Char: Monkeygirl
- Contato:
eu usei o google... mas foi dpois de algumas horas tentando e qbrando a cabeça ai eu li aki e vi q tinha um bug e fui atraz...
e se vocês perceberem tem um link no final do meu post dem uma olhada...
Lousy... o que eu quis dizer quando disse q não era impossivel foi q apareceu Win pra min... entendeu??? eu consegui matei a xarada... não importa como...
ahhh Aula de matemática só na escola... não to afim de aprender a Fórmula de Euler... muito obrigado...
e desculpa se te magoei xD...
não era minha intenção te tirar do sério...
como diz nossa ministra "Relaxa e Goza!".
e se vocês perceberem tem um link no final do meu post dem uma olhada...
Lousy... o que eu quis dizer quando disse q não era impossivel foi q apareceu Win pra min... entendeu??? eu consegui matei a xarada... não importa como...
ahhh Aula de matemática só na escola... não to afim de aprender a Fórmula de Euler... muito obrigado...
e desculpa se te magoei xD...
não era minha intenção te tirar do sério...
como diz nossa ministra "Relaxa e Goza!".

- Pereirao
- Macaco Admin

- Mensagens: 1806
- Registrado em: Qua Jan 07, 2004 10:17 am
- Sexo: Masculino
- Localização: São Paulo - SP - Brasil
- Contato:
Apesar de achar que esse assunto já rendeu muito, aqui vai.
Ouçam o Lousy, crianças... O problema, como é proposto, NÃO TEM SOLUÇÃO.
Aqui é uma solução válida, porém impraticável.

Ouçam o Lousy, crianças... O problema, como é proposto, NÃO TEM SOLUÇÃO.
Aqui é uma solução válida, porém impraticável.

Quem não ri de si mesmo, deixa esse trabalho para os outros...
Existem 10 tipos de pessoas: As que entendem binário e as que não entendem...
"Cada um cava a cova que consegue subir" (Ze_ninguém)








